Crypto CTF 2024
Some writeups of the challenges I solved in Crypto CTF 2024
Intro
Over the weekend of June 8 - June 9, the 6th CRYPTO CTF 2024 was held, and I decided to participate in it. This CTF was unique as it focused entirely on cryptography challenges. The challenges were categorized into five levels: Warm-up, Easy, Medium, Hard, and Tough. I aimed to test and improve my crypto skills throughout the competition.
RM2 - medium
Challenge
The RM2 cryptosystem is a minimalist design that exhibits remarkable resilience, making it exceptionally difficult to compromise. nc 00.cr.yp.toc.tf 13371
Level: Medium Resource: Here
Solution
You start with a zipped file containing one Python file named ‘RM2.py’ and a netcat address. Connecting to the netcat address displays the following Python code snippet:
This is the Python code provided for the challenge.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
#!/usr/bin/env python3
import sys
from Crypto.Util.number import *
from string import *
from random import *
from flag import flag
def die(*args):
pr(*args)
quit()
def pr(*args):
s = " ".join(map(str, args))
sys.stdout.write(s + "\n")
sys.stdout.flush()
def sc():
return sys.stdin.buffer.readline()
def randstr(l):
return ''.join([printable[randint(0, 90)] for _ in range(l)])
def encrypt(msg, p, q):
e = 65537
m1, m2 = msg[:len(msg) >> 1], msg[len(msg) >> 1:]
m1, m2 = bytes_to_long(m1), bytes_to_long(m2)
c1, c2 = pow(m1, e, (p - 1) * (q - 1)), pow(m2, e, (2*p + 1) * (2*q + 1))
return (c1, c2)
def main():
border = "┃"
pr( "┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┓")
pr(border, ".: Welcome to RM2 task! Your mission is break our cryptosystem :. ", border)
pr( "┗━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┛")
nbit, _b = 1024, False
pr(border, f"Please provide your desired {nbit}-bit prime numbers p, q:")
inp = sc().decode()
try:
p, q = [int(_) for _ in inp.split(',')]
if p.bit_length() == q.bit_length() == nbit and isPrime(p) and isPrime(q) and p != q:
_b = True
except:
die(border, f"The input you provided is is not valid!")
if _b:
e, n = 65537, p * q
s = randstr(nbit >> 4).encode()
m = bytes_to_long(s)
assert m < n >> 2
c1, c2 = encrypt(s, p, q)
pr(border, f'c1 = {c1}')
pr(border, f'c2 = {c2}')
pr(border, f'Now, send us the secret string to get the flag: ')
_m = sc().strip()
if _m == s:
die(border, f'Congrats, you got the flag: {flag}')
else:
die(border, f'The secret string is not correct! Bye!!')
else:
die(border, f"Your input does not meet the requirements!!!")
if __name__ == '__main__':
main()
Upon analysis, the program requires two 1024-bit prime numbers, p and q. It verifies if both p and q are prime, then proceeds to encrypt a randomly generated string using these numbers. It outputs two encrypted strings, c1 and c2. To obtain the flag, we need to decrypt these strings and input the decrypted message back into the netcat terminal.
Initially, I misunderstood the challenge and attempted to generate random prime numbers. However, this approach was unsuccessful 😂.
To generate prime numbers in Python, I started with a simple script:
1
2
3
4
5
6
7
8
9
10
11
12
13
from Crypto.Util.number import getPrime
def generate_primes(bits):
p = getPrime(bits)
q = getPrime(bits)
while p == q:
q = getPrime(bits)
return p, q
bits = 1024
p, q = generate_primes(bits)
print(f"{p},{q}")
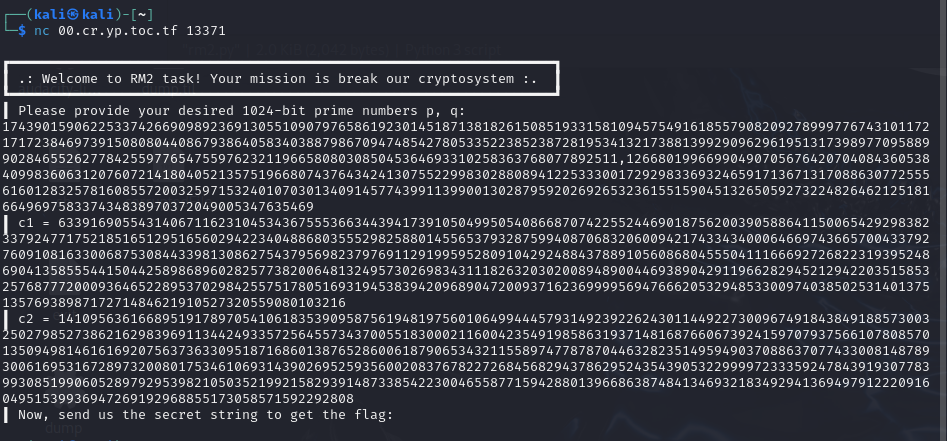
Everything seemed to be fine. I even got past the first hurdle and got the c1 and c2.
And thats where the problem started…..
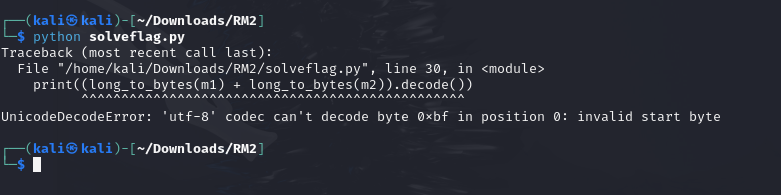
No matter how many times I generated and put a random prime number through it I kep getting the same error when trying to decode the
After a lot of investigation (chatgpt+youtube) I figured my mistake. Turns out for challenges like these you need to generate somethin called a ‘safe’ prime number to prevent the decoding error that keeps popping up for me.
So I rewrote the generateprimenumber script to generate safe prime numbers
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
import gensafeprime
from Crypto.Util.number import isPrime
ij = 1
def generate_safe_prime():
global ij
while True:
ij += 1
q = gensafeprime.generate(1024)
if isPrime(2 * q + 1):
return q
print(f"Try: {ij}")
# Generate the first safe prime
q1 = generate_safe_prime()
print(f"First safe prime q1: {q1}")
# Generate the second safe prime
q2 = generate_safe_prime()
print(f"Second safe prime q2: {q2}")
Quite simple since python has an in-built gensafeprime package which i exploited. But it does take quite some time to generate thoug so theres that. Just let the script run for about 10 mins.
Then I just had to figure out how to recover the original message. Turns out to be a simple math problem you just have to do it backwards to get to the source. Final script I used.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
from Crypto.Util.number import long_to_bytes, inverse
# Provided primes
p = YOUR_P_VALUE
q = YOUR_Q_VALUE
# Given ciphertexts
c1 = 13068168601849275327854521009952145570989001454974547389229964162543144165925105607203639033487063972656532424389179012127846568096073984759135307504510427081162734039232233380285719900851493658894946957702483924486192767175408718538497972558165097667860693238676523315282883160427329225389473834823102433625976956353216782743845098537310058217777418640967555730099483446150054033808186125096140963504009575245031624050302923828938347956436375744387335972046863017524436478996082056274637361641925332169399285753148497096428854654087525740083332660990775740769765495666994619667158268936414325543947365899424104567344
c2 = 26780381546498989908720655825587247204998098710015089040217024751646104521200105113694412785839569082038523161121328381317091578737444474331483335289912237138447351932170891693077785827128523828807461414798792550432799084346542208308764678207126546758539809984264618045536309213405191776330596066808620833730326132585926219478199916152049728951895930612422372801930863038230179951800816745643608320994238741018026894718816474185938108183879459525323156119005256640034787200951836843004399329875488304520824373891153100990372364680296073801784339663296573561203787576325791301241543690862025018429274633288641253550640
# Calculate moduli
n1 = (p - 1) * (q - 1)
n2 = (2 * p + 1) * (2 * q + 1)
# Public exponent
e = 65537
# Calculate private exponents
d1 = inverse(e, n1)
d2 = inverse(e, n2)
# Decrypt the messages
m1 = pow(c1, d1, n1)
m2 = pow(c2, d2, n2)
# Convert long integers to bytes
m1_bytes = long_to_bytes(m1)
m2_bytes = long_to_bytes(m2)
# Combine the halves to get the original string
original_message = m1_bytes + m2_bytes
print(f"The original message is: {original_message.decode()}")
AANNNDDDDD
Flag: CCTF{i_l0v3_5UpeR_S4fE_Pr1m3s !!}
Alibos - easy
Challenge
Alibos, a classic cryptographic algorithm, is designed to safeguard non-sensitive data, providing a reliable solution for routine information protection.
Level: Medium Resource: Here
Solution
Strted of with a encrypted file. When decrypted gives 2 files a alibis.py and output.txt. This one was slightly easier and much harder at the some. The main objective is to reverse the encryption process and to find the original message ‘m’. Use a ‘padded_chunk’ to find a part fo the original message. Search for the correct padding by iterating through possible initial values i and check if concatenated with padded_chunk is divisible by d**2. If true calculate m.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
from Crypto.Util.number import *
pkey = 8582435512564229286688465405009040056856016872134514945016805951785759509953023638490767572236748566493023965794194297026085882082781147026501124183913218900918532638964014591302221504335115379744625749001902791287122243760312557423006862735120339132655680911213722073949690947638446354528576541717311700749946777
enc = 6314597738211377086770535291073179315279171595861180001679392971498929017818237394074266448467963648845725270238638741470530326527225591470945568628357663345362977083408459035746665948779559824189070193446347235731566688204757001867451307179564783577100125355658166518394135392082890798973020986161756145194380336
d = len(str(pkey))
padded_chunk = 10**d + enc - pkey
for i in range(10000, 1000000):
candidate = int(str(i) + str(padded_chunk), 10)
if candidate % (d**2) == 0:
m = candidate // (d**2)
if str(m % (10**100)) == '1' * 100:
print(m)
print(long_to_bytes(m).decode()) # make sure to remove all the 1s at the end to prevent error popping up
break
1
2
3
4
┌──(kali㉿kali)-[~/Downloads/alibos]
└─$ python solve.py
6170704326493336128242608193100736601774626903966803036318189045381903593682775829229200905376968543264526051111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111
CCTF{h0M3_m4De_cRyp70_5ySTeM_1N_CryptoCTF!!!}
Flag: CCTF{h0M3_m4De_cRyp70_5ySTeM_1N_CryptoCTF!!!}
Finitura !!